نام: جمشید بن مسعود بن محمود طبیب کاشانی ملقب به غیاثالدین
نام به لاتین: Ghiyāth al-Dīn Jamshīd Masʿūd al-Kāshī
تولد: ۷۹۰ هجری قمری
درگذشت: 832 هجری قمری- سمرقند
شهرت: ریاضیدان، منجم
شرح زندگی:
غیاثالدین جمشید کاشانی (حدود ۷۹۰-۸۳۲) ریاضیدان برجسته، اخترشناس و شمارشگر زبردست ایرانی بود. نام کامل او عبارت است از جمشید بن مسعود بن محمود طبیب کاشانی ملقب به غیاثالدین که در غرب به الکاشی (al-kashi) مشهور است. او در عمر کوتاه خود آلات رصدی دقیقی اختراع کرد و از حدود ۸۰۸ (۱۴۰۶) تا پایان عمرش ۸۳۲ (۱۴۲۹) فعالیت علمی داشت و در دوران فعالیت علمیاش به نوشتن کتابهای گوناگونی در زمینهٔ ریاضیات و نجوم پرداخت.
غیاثالدین جمشید کاشانی هر چند فیزیکدان بود، ولی علاقهٔ اصلیاش متوجه ریاضیات و اخترشناسی بود؛ پس از دورهٔ طولانی بینوایی و سرگردانی، سرانجام در سایهٔ حمایت سلطان الغبیگ، که خود دانشمند بزرگی بود، موقعیت شغلی مطمئنی در سمرقند بهدست آورد.
غیاثالدین جمشید کاشانی، زبردستترین حسابدان و آخرین ریاضیدان برجستهٔ دورهٔ اسلامی و از بزرگترین مفاخر تاریخ ایران به شمار میآید. وی به تکمیل وتصحیح روشهای قدیمی انجام چهار عمل اصلی حساب پرداخت و روشهای جدید و سادهتری برای آنها اختراع کرد. در واقع، کاشانی را باید مخترع روشهای کنونی انجام چهار عمل اصلی حساب (به ویژه ضرب و تقسیم) دانست. کتاب ارزشمند وی با نام مفتاح الحساب کتابی درسی، دربارهٔ ریاضیات مقدماتی است و آن را از حیث فراوانی و تنوع مواد و مطالب و روانی بیان سرآمد همهٔ آثار ریاضی سدههای میانه میدانند.
جمشید ملقب به غیاثالدین، فرزند پزشکی کاشانی به نام مسعود حدود سال ۷۹۰ قمری (۱۳۸۸ میلادی)، در کاشان چشم به جهان گشود. او در همهٔ آثارش خود را چنین معرفی کردهاست:
کمترین بندگان خداوند (یا نیازمندترین بندگان خدا به رحمت او)، جمشید، پسر مسعود طبیب کاشانی، پسر محمود پسر محمد
بیشتر آنچه که از زندگی وی میدانیم از بررسی آثار علمی ارزندهاش و نیز دو نامهای که خطاب به پدر خود و مردم کاشان نوشته به دست آمدهاست.
دوران کودکی و جوانی وی درست همزمان با اوج یورشهای وحشیانهٔ تیمور به ایران بود. با وجود این، جمشید در همین شرایط نیز هرگز از آموختن غافل نشد. پدرش مسعود، چنانکه گفتیم، پزشک بود اما شاید از علوم دیگر نیز بهرهٔ بسیار داشت. برای نمونه، از یکی از نامههای کاشانی به پدرش معلوم میشود که پدر قصد داشته تا شرحی بر معیار الاشعار نصیرالدین طوسی بنویسد و برای پسر، یعنی جمشید بفرستد.
نخستین فعالیت علمی کاشانی که از تاریخ دقیق آن آگاهیم، رصد خسوف در ۱۲ ذیحجهٔ ۸۰۸ قمری، برابر با دوم ژوئن ۱۴۰۶ میلادی در کاشان است. غیاثالدین نخستین اثر علمی خود را در همین شهر و در ۲۱ رمضان ۸۰۹ قمری مطابق با اول مارس ۱۴۰۷ میلادی، یعنی ۲ سال پس از مرگ تیمور و فرو نشستن فتنهٔ او، نوشت. چهار سال بعد در ۸۱۳ قمری هنوز در کاشان بود و رسالهٔ مختصری به فارسی دربارهٔ کیهانشناسی (علم هیأت) نوشت. در ۸۱۶ قمری کتاب نجومی مهم خود «زیج خاقانی» را به فارسی نوشت و به اُلُغْ بیگ، فرزند شاهرخ و نوهٔ تیمور، که در سمرقند به سر میبرد، هدیه کرد. کاشانی امید داشت که با حمایت الغ بیگ بتواند با آسودگی بیشتر پژوهشهای علمی خود را ادامه دهد.
کاشانی دست کم تا مدتی پس از پدیدآوردن کتاب ارزشمند «تلخیص المفتاح»، یعنی ۷ شعبان ۸۲۴ قمری مطابق با ۷ اوت ۱۴۲۱ میلادی، هنوز در کاشان به سر میبرد. این نکته خود مایهٔ شگفتی بسیار است که چرا مردی دانشور چون الغ بیگ پس از مطالعهٔ زیج خاقانی به نبوغ کمنظیر پدیدآورندهٔ آن پی نبرد! کاشانی در یکی از دو نامهٔ خود از یک سو به طور تلویحی از این که بسیار دیر مورد توجه دولتمردان قرار گرفته گلایه میکند و از سوی دیگر از اینکه پس از این مدت دراز به شهری چون سمرقند دعوت شدهاست، سر از پا نمیشناسد.
کاشانی به احتمال قوی در ۸۲۴ قمری به همراه معینالدین کاشانی (همکار غیاثالدین در کاشان و سمرقند) از کاشان به سمرقند رفت و چنان که خود در نامههایش کم و بیش اشاره کرده، در پیریزی رصدخانهٔ سمرقند نقش اصلی را ایفا نمود. از همان آغازِ کار، وی را به ریاست آنجا برگزیدند و تا پایان عمر به نسبت کوتاه خود در همین مقام بود.
مرگ
کاشانی سرانجام صبح روز چهارشنبه ۱۹ رمضان ۸۳۲ قمری برابر با ۲۲ ژوئن ۱۴۲۹ میلادی بیرون شهر سمرقند و در محل رصدخانه درگذشت. امین احمد رازی در کتاب تذکرهٔ هفت اقلیم میگوید که چون کاشانی چنان که باید و شاید آداب حضور در دربار را رعایت نمیکرد، الغ بیگ فرمان به قتل او داد.
از نامههای کاشانی به پدرش چنین برمیآید که پدر به دلایلی از سرنوشت فرزند خود در دربار الغ بیگ نگران بود و در نامه یا نامههایی، پسر را از خطرات معمول در دربار پادشاهان برحذر داشته بود و کاشانی نیز در پاسخ برای کاستن از نگرانیهای پدر، نمونههای متعددی از توجه خاص الغ بیگ به خود را برای پدر شاهد آورده بود.
مهمترین دستاوردها
ابداع و ترویج کسرهای اعشاری به قیاس با کسرهای شصتگانی که در ستارهشناسی متداول بود. محاسبهٔ عدد پی تا شانزده رقم اعشار به نحوی که تا صد و پنجاه سال بعد کسی نتوانست آن را گسترش دهد: ۲π=۶٫۲۸۳۱۸۵۳۰۷۱۷۹۵۸۶۵
محاسبه سینوس (جیب) زاویهٔ یک درجه با روش ابتکاری حل یک معادلهٔ درجه سوم (sin۱=.۰۱۷۴۵۲۴۰۶۴۳۷۲۸۳۵۱۰۳۷۱۲) که هفده رقم اعشاری عدد به دست آمده با مقداری که امروزه محاسبه میشود همخوانی دارد. در واقع کاشانی مقدار سینوس یک درجه را تا ده رقم صحیح شصتگانی حساب کرد. (به کمک فرمول زیر: )
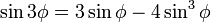
اختراع ابزار اخترشناسی دقیق از جمله وسیلهای به نام «طبق المناطق» برای محاسب طول ستارگان که کتاب نزهتالحدائق در شرح آن است.
نوآوریهای کاشانی
- اختراع کسرهای دهگانی (اعشاری). گرچه کاشانی نخستین به کار برندهٔ این کسرها نیست، اما بیتردید رواج این کسرها را به او مدیونیم.
- دستهبندی معادلات درجهٔ اول تا چهارم و حل عددی معادلات درجهٔ چهارم و بالاتر
- محاسبهٔ عدد پی. کاشانی در الرسالة المُحیطیة (ص ۲۸)، عدد π را با دقتی که تا ۱۵۰ سال پس از وی بینظیر ماند محاسبه کردهاست.
- تکمیل و تصحیح روشهای قدیمی انجام چهار عمل اصلی و اختراع روشهای جدیدی برای آنها. در واقع، کاشانی را باید مخترع روشهای کنونی انجام چهار عمل اصلی حساب (به ویژه ضرب و تقسیم) دانست.
- اختراع روش کنونی پیدا کردن ریشهٔ n اُم عدد دلخواه. روش کاشانی در اصل همان روشی است که صدها سال بعد توسط پائولو روفینی (ریاضیدان ایتالیایی، ۱۷۶۵-۱۸۲۲میلادی) و ویلیام جُرج هارنر (ریاضیدان انگلیسی، ۱۷۸۶-۱۸۳۷میلادی)، باردیگر اختراع شد.
- اختراع روش کنونی پیدا کردن جذر (ریشهٔ دوم) که در اصل ساده شدهٔ روش پیدا کردن ریشهٔ n اُم است.
- ساخت یک ابزار رصدی. کاشانی ابزارِ رصدی جالبی اختراع کرد و آن را طَبَقُ المَناطِقْ نامید. رسالهای نیز به نام نُزْهَةُ الحَدائِق دربارهٔ چگونگی کار با آن نوشت.
- تصحیح زیج ایلخانی. کاشانی زیج خاقانی را نیز در تصحیح اشکالات زیج ایلخانی نوشت.
- نگارش مهمترین کتاب دربارهٔ حساب. کتاب مفتاح الحساب کاشانی مهمترین و مفصلترین اثر دربارهٔ ریاضیات عملی و حساب در دورهٔ اسلامی است.
- محاسبهٔ جِیب یک درجه. کاشانی در رسالهٔ وَتَر و جِیب مقداری برای جِیبِ یک درجه (۶۰ sin ۱˚) به دست آورده که اگر آن را بر ۶۰ تقسیم کنیم، حاصل آن تا ۱۷ رقم اعشاری با مقدار واقعی سینوس یک درجه موافق است.
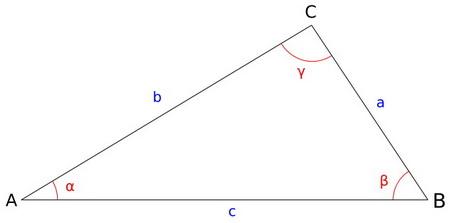
قانون کاشانی (قانون کسینوس)
در مثلثات قانون کسینوس که به نام قانون کاشانی هم شناخته میشود و در مورد هر نوع مثلثی صدق میکند به این شکل است:
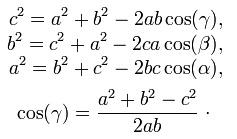
آثار کاشانی
سُلّمُ السَماء (نردبان آسمان) یا رسالهٔ کمالیه به عربی. کاشانی این رساله را در ۲۱ رمضان ۸۰۹ قمری (اول مارس ۱۴۰۷ میلادی) در کاشان به پایان رساندهاست. کاشانی در این رساله از قطر زمین، قطر خورشید، ماه، سیارات، و ستارگان و فاصلهٔ آنها از زمین سخن گفتهاست.
مختصر در علم هیأت به فارسی. کاشانی این رساله را در ۸۱۳ قمری برابر با ۱۴۱۰ میلادی، یا اندکی پیش از آن نوشت. وی در این رساله دربارهٔ مدراهای ماه، خورشید، ستارگان، و سیارهها و چگونگی حرکت آنها سخن گفتهاست.
زیج خاقانی به فارسی: این کتاب یکی از آثار مهم نجومی کاشانی به شمار میرود. کاشانی این زیج را در ۸۱۶ قمری (۱۴۱۳ میلادی) کامل کرد. هدف کاشانی از نگارش این زیج، تصحیح اشتباهاتی است که در زیج ایلخانی روی دادهاست. کاشانی در مقدمهٔ زیج خود با به رغم انتقاد از مطالب زیج ایلخانی، از نویسندهٔ آن، خواجه نصیرالدین طوسی، با تجلیل و احترام بسیار یاد کردهاست.
شرح آلات رَصَد به فارسی: کاشانی این رساله را در ذیقعدهٔ ۸۱۸ قمری(ژانویهٔ ۱۴۱۶ میلادی) برای شخصی به نام سلطان اسکندر نوشتهاست. برخی این اسکندر را «اسکندر بن قرایوسف قراقویونلو» دانستهاند. اما برخی دیگر، معتقدند که این اسکندر، پسر عموی الغ بیگ است که بر فارس و اصفهان حکومت میکردهاست.
نُزْهَةُ الحَدائِق به عربی: کاشانی این رساله را در دهم ذیحجهٔ ۸۱۸ قمری مطابق ۱۰ فوریهٔ ۱۴۱۶ میلادی (حدود یک ماه پس از نگارش رسالهٔ شرح آلات رصد) نوشته و در آن دستگاهی به نام طبق المناطق را که اختراع خود وی بوده، شرح دادهاست. با این دستگاه میتوان محل ماه و خورشید و پنج سیارهٔ شناخته شده تا آن زمان و نیز فاصلهٔ هر یک از آنها را تا زمین، و برخی پارامترهای سیارهای دیگر را به دست آورد.
ذِیلِ نزهة الحدائق. کاشانی در نیمهٔ شعبان ۸۲۹ قمری (۲۲ ژوئن ۱۴۲۶ میلادی) و هنگامی که در سمرقند اقامت داشته، ده «اِلْحاق» (پیوست) را به نزهة الحدائق افزودهاست.
تَلْخیصُ المِفْتاح به عربی. این رساله، چنان که از نامش پیداست گزیدهٔ مفتاح الحساب کاشانی است. کاشانی کار تلخیص را در ۷ شعبان ۸۲۴ قمری (۷ اوت ۱۴۲۱ میلادی) به پایان رساندهاست. وی در مقدمهٔ این رساله چنین آوردهاست: «اما بعد، نیازمندترین بندگان خداوند به بخشایش وی، جمشید ملقب به غیاث، پسر مسعود پزشک کاشانی، پسر محمود، که خداوند روزگارش را نیکو گرداند، گوید که چون از نگارش کتابم موسوم به مفتاح الحساب فارغ شدم، آن دسته از مطالب این کتاب را که دانستن آنها برای نوآموزان واجب است در این مختصر گرد آوردم و آن را تلخیص المفتاح نامیدم.»
الرِسالةُ المُحیطیة به عربی. کاشانی این رساله را که یکی از مهمترین آثار اوست در اواسط شعبان ۸۲۷ قمری (ژوئیهٔ ۱۴۲۴ میلادی) به پایان رساندهاست. وی در این رساله نسبت محیط دایره به قطر آن، یعنی عدد پی را به دست آوردهاست.
وَتَر و جِیب، کاشانی این رسالهٔ را دربارهٔ چگونگی محاسبهٔ جِیب یک درجه نوشتهاست. شوربختانه متن اصلی این رساله باقی نمانده اما از شرحهایی که بر آن نوشتهاند میتوان به مطالب آن پی برد.
زیج تَسْهیلات، کاشانی این اثر را پیش از ۸۳۰ قمری تألیف کردهاست زیرا در مقدمهٔ مفتاح الحساب از این کتاب نام برده(ص ۳۶) ولی تا کنون وجود نسخهای قطعی از آن گزارش نشدهاست.
مفتاح الحساب
کاشانی کار نگارش مفتاح الحساب را، که بیتردید مهمترین، مفصلترین و برجستهترین کتابِ ریاضیات عملی در دورة اسلامی بشمار میآید، در ۳ جمادی الاولی سال ۸۳۰ قمری برابر با ۲ مارس ۱۴۲۷ میلادی به پایان رسانده و آن را به الغ بیگ هدیه کردهاست. اما پیشنویس این کتاب را دست کم از ۶ سال پیش، یعنی ۸۲۴ قمری فراهم آورده و در این مدت، مشغول تکمیل و اصلاح آن بودهاست. زیرا او در مقدمهٔ تلخیص المفتاح که در همین سال نوشته شده، تأکید کرده که این تلخیص را پس از به پایان رساندن تألیف مفتاح الحساب فراهم آوردهاست.
برای نشان دادن اهمیت مفتاح الحساب کاشانی نزد شرق شناسان، بویژه محققان اروپایی، در اینجا به چاپهای مختلف متن عربی و ترجمههای این اثر اشاره میکنیم:
در ۱۸۶۴ میلادی فرانتس ووپکه، محقق آلمانی الاصل ساکن فرانسه، بخشی از این کتاب را به فرانسه ترجمه کرد.
در ۱۹۴۴ میلادی، پاول لوکی بخش قابل توجهی از مفتاح الحساب را به آلمانی ترجمه و شرح کرد. این ترجمه نیز، همچون ترجمهٔ رسالة محیطیه، پس از مرگ لوکی و در سال ۱۹۵۱ میلادی منتشر شد. وی همچنین مقالهٔ مهمی دربارهٔ روش کاشانی در پیدا کردن ریشهٔ n اُم اعداد نوشت.
در ۱۹۵۱ میلادی نائله رجایی در پایاننامهٔ دورهٔ دکترای خود در دانشگاه آمریکایی بیروت، با استفاده از مطالب مفتاح الحساب و رسالة محیطیه به بحث دربارهٔ اختراع کسرهای اعشاری توسط کاشانی پرداخت.
در همان سال و در همان دانشگاه، عبدالقادر الداخل نیز در پایاننامهٔ دکترای خود روش کاشانی دربارهٔ پیدا کردن ریشهٔ n اُم در دستگاه شمار شصتگانی بررسی کرد.
در ۱۹۵۶ میلادی نیز برویس رُزنفلد، آدُلف یوشکویچ، و سِگال، تصویر یک نسخهٔ خطی این اثر و نیز تصویر یک نسخهٔ خطی رسالهٔ محیطیهٔ را همراه با ترجمهٔ روسی آن در مسکو به چاپ رساندند.
در ۱۹۶۷ میلادی احمد سعید الدمرداش و محمد حمدی الحفنی الشیخ، متن عربی این کتاب را در قاهره به چاپ رساندند. غلطهای این چاپ حتی از غلطهای نسخهٔ خطی چاپ مسکو بیشتر است.
در ۱۹۷۷ میلادی نادر النابلسی یک بار دیگر تمامی این کتاب را با حواشی به نسبت سودمند و با دقتی بیشتر از دو مصحح قبلی در دمشق به چاپ رساند.
گفتنی است که در هیچ یک از ترجمهها یا چاپهای یاد شده از نسخهٔ خطی کتابخانهٔ ملی ملک، که کهنترین و بهترین نسخهٔ موجود مفتاح الحساب به بشمار میآید استفاده نشدهاست.
نظرات دانشمندان معاصر:
پاول لوکی، پژوهشگر برجستهٔ آلمانی که بیش از هر تاریخ شناس دیگری در راه شناساندن ارزش آثار ریاضی این دانشمند بزرگ به جهان کوشش کرده، دربارهٔ آثار کاشانی چنین آوردهاست:
پس از پژوهش دربارهٔ برخی آثار کاشانی، که خوشبختانه بیشتر آنها در کتابخانههای شرق و غرب موجود است، او را ریاضیدانی هوشمند، مخترع، نَقّاد و صاحب افکار عمیق یافتم. کاشانی از آثار ریاضیدانان پیش از خود آگاه و بویژه در فن محاسبه و به کار بستن روشهای تقریبی بسیار آگاه و چیرهدست بودهاست. اگر رسالهٔ محیطیه او به دست ریاضیدانان غربی معاصر وی رسیده بود، از آن پس مردم مغرب زمین از بعضی منازعات و تألیفات مبتذل دربارهٔ اندازهگیری دایره (محاسبهٔ عدد پی) بینیاز میشدند. اگر نظریهٔ واضح و روش علمی وی در مورد شناساندن کسرهای اعشاری انتشار یافته بود، فرانسوا وییتْ، اِستِوِن، و بورگی ناچار نمیشدند که یک قرن و نیم پس از کاشانی نیروی فکری و عملی خود را برای از نو یافتن این کسرها به کار اندازند.
اِدوارد اِستوارت کنِدی، پژوهشگر برجستهٔ آمریکایی، که مدتی نیز در ایران میزیستهاست و با زبان فارسی آشنایی دارد دربارهٔ کاشانی چنین گفتهاست:
پیش از هر چیز باید گفت که کاشانی حاسبی زبردست بود و در این فن مهارت شگفت انگیزی داشت. و شاهد این مدعا این است که وی با اعداد شصتگانی خالص به آسانی و روانی حساب میکرد. کسرهای اعشاری را اختراع نمود، روش تکراری را در حساب به طور کامل و پیگیر به کار میبست. با چیره دستی مراحل محاسبه را طوری تنظیم مینمود که بتواند حداکثر مقدار خطا را پیشبینی کند و در هر جا درستی اعمال را امتحان میکرد.
آدُلف یوشکویچ، پژوهشگر مشهور روسیه در کتاب تاریخ ریاضیات در سدههای میانه در بارهٔ کتاب ارزشمند کاشانی مینویسد:
مفتاح الحساب کتابی درسی، دربارهٔ ریاضیات مقدماتی است که استادانه تألیف شده و مؤلف آنچه را که طبقات مختلف خوانندگان کتاب بدان نیاز داشتهاند، در نظر گرفتهاست. این کتاب از حیث فراوانی و گوناگونی مواد و مطالب و روانی بیان تقریباً در همهٔ آثار ریاضی سدههای میانه یگانهاست.
مهمترین تالیفات:
- در زمینهٔ ریاضیات
مفتاح الحساب
رسالهٔ محیطیه
رساله وتر و جیب
- در زمینهٔ اخترشناسی
زیگ خاقانی در تکمیل زیگ ایلخانی تالیف نصیرالدین طوسی (به فارسی)
زیج التهسیلات
نزهت الحدایق شرح دو ابزاری که خود اختراع کرده بود، طولیاب سیارهای، و دستگاهی برای اجرای درونیابی خطی، میپردازد.

عکس صفحهٔ آخر رسالهٔ محیطیه
موجود در کتابخانهٔ آستان قدس رضوی شماره ۲۲۹.
منبع: دانشنامه فارسی ویکیپدیا
کرامتی، یونس. در قلمرو ریاضیات، بازنویسی و تلخیص کتاب مفتاح الحساب غیاث الدین جمشید کاشانی. چاپ دوم. تهران: اهل قلم، ۱۳۸۲.
معرفی کتاب:
زندگی نامه غیاث الدین جمشید کاشانی ریاضی دان و منجم بزرگ ایرانی
گردآوری: ابوالقاسم قربانی
نام کتاب: کاشانی نامه
تعداد صفحه: 306
نشر: زعیم (23 آبان، 1390)