اصل شمول و عدم شمول

در ترکیبات اصل شمول و عدم شمول¹ (اصل شمول - طرد) اگر A و B دو مجموعه متناهی (۲=n) باشند، آنگاه

$|A \cup B| = |A| + |B| - |A \cap B| \,$

اصل شمول و عدم شمول یک قضیه (قابل اثبات) است، اما به علت سادگی، به عنوان یک اصل بیان می‌شود.

اثبات

A را اجتماع $\scriptstyle \cup_{i=1}^n A_i$ از مجموعه‌های A₁,...,A_n در نظر می‌گیریم. برای اثبات اصل شمول و عدم شمول در حالت عام، اول باید مشخصات

$1_A =\sum_{k=1}^n (-1)^{k-1}\sum_{\scriptstyle I\subset\{1,\ldots,n\}\atop\scriptstyle|I|=k} 1_{A_I}\qquad(*)$

را برای توابع مشخصه به صورت

$A_I = \bigcap_{i\in I} A_i$

بررسی کنیم. حداقل دو راه برای این کار هست:

راه اول: کافی است برای هر x xدر اجتماع A₁,...,A_nاین کار را بکنیم. فرض کنیم دقیقا به m تا از مجموعه‌ها تعلق دارد (۱ ≤ m ≤ n). برای سادگی این مجموعه‌ها را A_۱، ...، A_m در نظر می‌گیریم. پس مشخصه در x به

$1 =\sum_{k=1}^m (-1)^{k-1}\sum_{\scriptstyle I\subset\{1,\ldots,m\}\atop\scriptstyle|I|=k} 1$

کاهش می‌یابد.

تعداد زیرمجموعه‌های kعضوی از مجموعه mعضوی برابر با 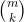$\textstyle\binom mk$ است. چون $\textstyle1=\binom m0$ ٬

$\binom m0 =\sum_{k=1}^m (-1)^{k-1}\binom mk$

با قرار دادن همهٔ جملات در سمت چپ معادله، بسط (۱ – ۱)^m را با استفاده از بسط دو جمله‌ای به دست می‌آوریم. بنابراین (*) برای x صادق است.

راه دوم: تابع زیر همیشه صفر است

$(1_A-1_{A_1})(1_A-1_{A_2})\cdots(1_A-1_{A_n})\,=\,0\,$

زیرا: اگر x در A نباشد، آنگاه تمام پرانتزها صفر می‌شوند (۰ - ۰ = ۰). در غبر این صورت، اگر x متعلق به A_m باشد، پرانتز mام صفر می‌شود (۱ - ۱ = ۰). با بسط ضرب در سمت راست به معادلهٔ (*) می‌رسیم.

استفاده از (*): برای اثبات اصل شمول و عدم شمول برای اندازهٔ مجموعه‌ها، معادلهٔ (*) را برای تمام xها در اجتماع A_۱، ...، A_n جمع می‌کنیم.

یک مثال

مثال) فرض کنید { S = { ۱،۲، … ، ۱۰۰، چند عضو از S وجود دارد که بر ۲ و ۵ بخش نباشد؟

حل) تعداد اعدادی که مضرب 2 هستند: ۵۰

تعداد اعدادی که مضرب 5 هستند: ۲۰

تعداد اعدادی که مضرب 2 و 5 هستند: ۱۰

جواب:

= ۱۰ + ۲۰ - ۵۰ - ۱۰۰ ۴۰

پی نوشت...

1. The Inclusion-Exclusion Principle

منبع

کتاب ترکیبات انتشارات فاطمی، علیرضا علیپور

کلمات کلیدی

اصل شمول - طرد اصل شمول - عدم شمول

آی هوش: گنجینه دانستنی ها و معماهای هوش و ریاضی

نظراتی که درج می شود، صرفا نظرات شخصی افراد است و لزوماً منعکس کننده دیدگاه های آی هوش نمی باشد.

آی هوش: مرجع مفاهیم هوش و ریاضی و انواع تست هوش، معمای ریاضی و معمای شطرنج

در زمینه‌ی انتشار نظرات مخاطبان، رعایت برخی موارد ضروری است:

-- لطفاً نظرات خود را با حروف فارسی تایپ کنید.
-- آی هوش مجاز به ویرایش ادبی نظرات مخاطبان است.
-- آی هوش از انتشار نظراتی که در آنها رعایت ادب نشده باشد معذور است.
-- نظرات پس از تأیید مدیر بخش مربوطه منتشر می‌شود.

نظر شما

ارسال